作业中的一道题,万恶之源←_←
利用 Huffman 编码进行通信可以大大提高信道利用率,缩短信息传输时间,降低传输成本。但是,这要求在发送端通过一个编码系统对待传数据预先编码,在接收端将传来的数据进行译码。对于双工信道(即可以双向传输信息的信道),每端都需要一个完整的编码、译码系统。试为这样的信息收发站写一个 Huffman 的编码、译码系统。
一个完整的系统应具有以下功能:
- 初始化。从终端读入字符集大小 n,以及 n 个字符和 n 个权值,建立 Huffman 树,并将它存在于文件 Huffman 中。
- 编码。利用以建好的 Huffman 树(如不在内存,则从文件 Huffman 中读入),对文件的正文进行编码,然后将结果存入文件 CodeFile 中。
- 译码。利用已建好的 Huffman 树将文件 CodeFile 中的代码进行译码,结果存入在文件 TextFile 中。
利用教科书 P148 例 6-2 中数据调试程序。
生成 Huffman 树
《数据结构(C 语言版)》书上给出了完整的 Huffman 编码算法,不过我把它拆成了两部分:生成 Huffman 树、根据 Huffman 树生成 Huffman 编码。
//HT存放构造的H树
//HC存放构造的编码
//w指向存放了每个字符的权的数组
//n是字符数量
//把建树和编码的部分分开了
void HuffmanCoding(HuffmanTree *HT, HuffmanCode *HC, unsigned int *w, unsigned int n) {
//只有一个或者没有字符还有什么编码的必要吗?
if (n <= 1) return;
InitHuffmanTree(HT, w, n);
InitHuffmanCode(HC, *HT, n);
}先总结一下生成 Huffman 树的基本原理~
- 为每个字符生成一个单独的叶子结点:结点的权就是字符的权,左右子树和双亲都是空的。(实际上这个单独的结点就是一个二叉树,结点本身就是它的根结点)
- 新建一个结点作为根结点,从所有双亲为空的结点(实际上也是某个树的根结点)中找出权最小的两个作为左右子树,“合并”成一个二叉树。
- 一直循环上一步,直到只剩下一个二叉树为止。一开始有 n 个字符(叶子结点)的话,最终的结点总数一定是 2n-1 个( ‘-ωก̀ )
经过以上过程就可以得到一个新鲜出炉的 Huffman 树了~(っ´ω`)ノ
以下代码几乎完全照抄书上的示例,我只是尝试着加上了一些注释。
void InitHuffmanTree(HuffmanTree *HT, unsigned int *w, unsigned int n) {
unsigned int m = 2 * n - 1; //H树一共有2n-1个节点
*HT = malloc((m + 1) * sizeof(HTNode)); //留一个0号结点表示指向空树,相当于二叉树中的NULL
//为每个字符构建只有根结点,没有左右子树的二叉树
(*HT)[0].weight = 0; (*HT)[0].parent = 0;
(*HT)[0].lchild = 0; (*HT)[0].rchild = 0;
HTNode *p = *HT + 1; //从1号结点开始
unsigned int i = 1;
while (i <= n) {
(*p).weight = *w; (*p).parent = 0;
(*p).lchild = 0; (*p).rchild = 0;
i++; p++; w++;
}
//剩下的树是空树
while (i <= m) {
(*p).weight = 0; (*p).parent = 0;
(*p).lchild = 0; (*p).rchild = 0;
i++; p++;
}
//开始生成H树
unsigned int s1, s2;
for (i = n + 1; i <= m; i++) {
//从所有双亲为空的结点(实际上也是某个树的根结点)中找出权最小的两个,编号保存到s1和s2
//书上并没有详细给出这里的操作,下面的算法是我自己瞎写的~
Select(*HT, i - 1, &s1, &s2);
(*HT)[s1].parent = i; (*HT)[s2].parent = i;
(*HT)[i].lchild = s1; (*HT)[i].rchild = s2;
(*HT)[i].weight = (*HT)[s1].weight + (*HT)[s2].weight;
}
}
void Select(HuffmanTree HT, unsigned int range, unsigned int *s1, unsigned int *s2) {
unsigned int v1 = 4294967295, v2 = 4294967295; //v1和v2保存s1和s2两个下标对应的权,初始值为unsigned int的最大值
*s1 = 0; *s2 = 0; //初始化s1和s2的值
for (unsigned int i = 1; i <= range; i++) {
if (HT[i].parent) continue; //只在双亲为空的结点中查找
if (HT[i].weight < v1) {
v2 = v1;
v1 = HT[i].weight;
*s2 = *s1;
*s1 = i;
} else if (HT[i].weight < v2) {
v2 = HT[i].weight;
*s2 = i;
}
}
//保证s1<s2
v1 = *s1; v2 = *s2;
*s1 = (v1 < v2) ? v1 : v2; *s2 = (v1 > v2) ? v1 : v2;
}0 号结点是空的,相当于指针里的 NULL,1 ~ n 号结点是一开始为每个字符生成的叶子结点,n ~ 2n-1号结点是“合并”的过程中生成的结点,图中的 n 是 8。
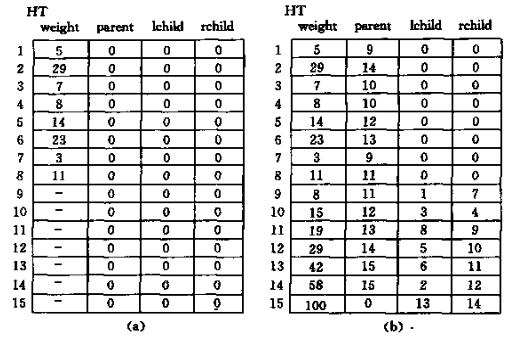
嗯……这个 Huffman 树好像很像一个数组?所以可以用一个 fwrite() 把 Huffman 树整个保存下来。当然,由于这个程序还需要对实际的字符进行编码解码,而 Huffman 树本身不存储字符信息,所以还需要把字符集的信息也保存进来(っ‘-’)╮
fopen_s(&fpHuff, "Huffman.bin", "wb");
//保存字符集信息
fwrite(&CharSetSize, sizeof(unsigned int), 1, fpHuff);
fwrite(CharSet, sizeof(char), CharSetSize, fpHuff);
fwrite(CharWeight, sizeof(unsigned int), CharSetSize, fpHuff);
//保存Huffman树。字符有n个,则一共有2n-1个结点,再加上一个空的0号结点就是2n个。
fwrite(HT, sizeof(HTNode), 2 * CharSetSize, fpHuff);
fclose(fpHuff);根据树生成编码表
以下是生成一个字符的 Huffman 编码的过程~
- 将一个指针指向表示字符的叶子结点。
- 将指针一直往上移,移到 Huffman 树的根结点为止。
- 从左/右子树往上移一层,就在编码中输出一个 0/1,这个生成顺序是逆向的。
随便做了一个动图,展示一下生成编码的过程_(:зゝ∠)_
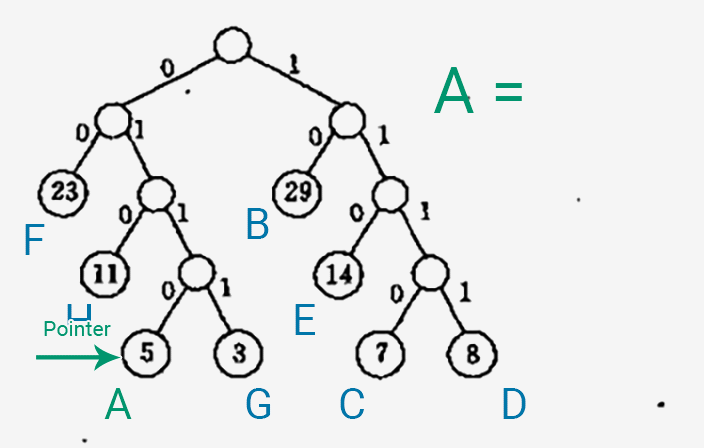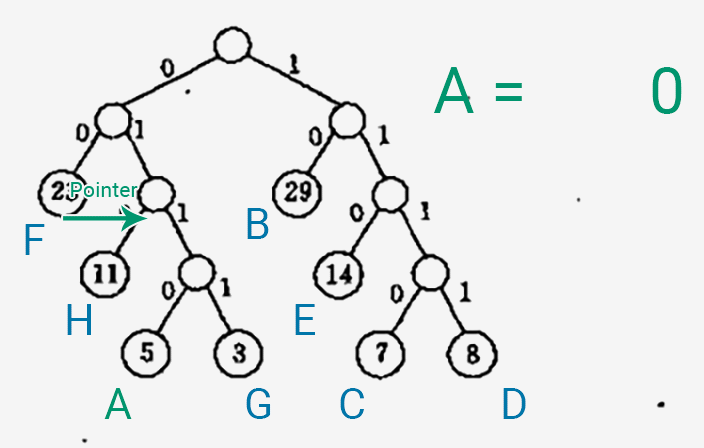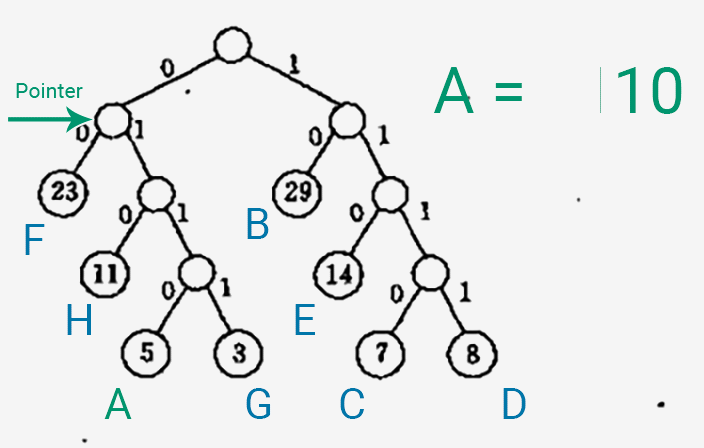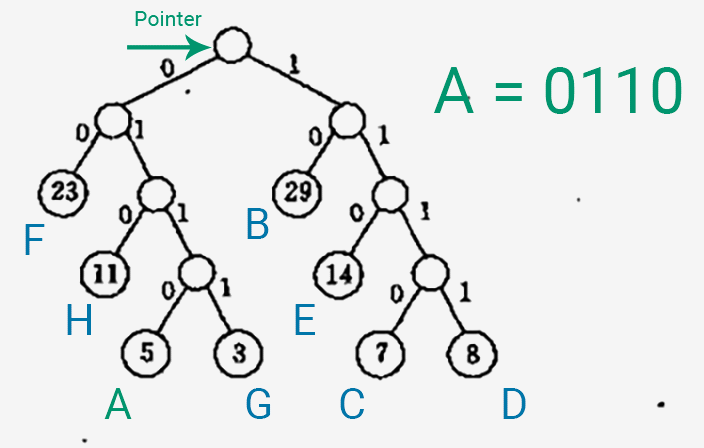
以下代码还是几乎完全照抄书上的示例,我只是尝试着加上了一些注释。
void InitHuffmanCode(HuffmanCode *HC, HuffmanTree HT, unsigned int n) {
*HC = malloc((n + 1) * sizeof(char*)); //HC相当于一个由字符数组组成的数组
char *cd = malloc(n * sizeof(char)); //求编码的工作区
cd[n - 1] = '\0'; //字符数组以\0结尾
unsigned int start; //表示一个编码从cd的哪一项开始
unsigned int c, f; //c指当前指向的树,f是c的双亲
//对每个字符逆向求编码
for (unsigned int i = 1; i <= n; i++) {
start = n - 1;
//求编码从叶子结点开始,到c指向根结点为止,此时f为0
for (c = i, f = HT[i].parent; f != 0; c = f, f = HT[f].parent) {
start--; //向前移一位
if (HT[f].lchild == c) {
cd[start] = '0'; //左子树的路径用0表示
} else {
cd[start] = '1'; //右子树的路径用1表示
}
}
//从cd复制到HC
(*HC)[i] = malloc((n - start) * sizeof(char));
strcpy_s((*HC)[i], n - start + 1, &cd[start]);
}
free(cd);
}对文本进行编码和解码
在上面的代码中,保存的编码其实是字符 0 和 1。简单的做法是编码的时候直接输出一大堆 0 和 1 两种字符,不过因为我实在是没什么事干,就选择了比较困难的做法:输出对应的二进制位。
编码表本身需不需要用二进制位存储?我觉得没必要啦~꜀(。௰。 ꜆)꜄
C++ 有个叫 bitset 的结构可以存储二进制位,不过 C 语言是没有的,所以只能自己查一下位运算的资料(相关内容出现在“谭宝书”的“学习辅导”分册,并不是课内的内容),自己造了两个轮子ε-(•́ω•̀๑)
//对位进行相关操作
//这里的unsigned char对于位是0或1,对于偏移是0到7
//设byte为10101100(对应offset为76543210),即172,读取offset为5的位
//offset=5
//00100000 1<<offset
//10101100 byte
//00100000 byte&(1<<offset)
//00000001 (byte&(1<<offset))>>offset
unsigned char ReadBit(unsigned char byte, unsigned char offset) {
return (byte & (1 << offset)) >> offset;
}
//设byte为10101100(对应offset为76543210),即172,将offset为4的位改为1
//offset=4 write=1
//00010000 write<<offset
//10101100 byte
//10111100 byte|(write<<offset)
void WriteBit(unsigned char *byte, unsigned char offset, unsigned char write) {
*byte |= write << offset;
}C 语言对变量的读写,最小也只能以一个字节为单位。为了对二进制位进行读写,我的想法是使用一个指针指向需要读写的那个位所在的字节,以及一个偏移量用来指定读写的是这个字节的第几位(´゚ω゚`) 另外,输出的二进制位不一定能凑满一个完整的字节,这时就将剩下的位设为 0,凑出一个完整的字节,同时再用一个整数保存二进制位的数量。
所以编码的代码大概是这个样子~
之前说过,我把书上的编码算法拆成了生成 Huffman 树和生成编码表两个部分。因为编码表本身是不需要保存的,在编码和解码的时候,根据 Huffman 树现场生成就可以了|ω•`)
//读取Huffman树过程略
//变量定义略,自己判断变量类型咯~
//根据Huffman树建立编码表
InitHuffmanCode(&HC, HT, CharSetSize);
//读取TextFile
fopen_s(&fpCode, "CodeFile.bin", "wb");
fopen_s(&fpText, "TextFile.txt", "rb");
//获取TextFile的大小
fseek(fpText, 0L, SEEK_END);
FileSize = ftell(fpText);
fseek(fpText, 0L, SEEK_SET);
CodeSize = 0;
Offset = 7;
Byte = 0;
//对TextFile中的每个字符进行编码
for (unsigned long long i = 0; i < FileSize; i++) {
Status = 1;
fread(&Read, sizeof(char), 1, fpText);
//从编码表中查找对应的编码,pCode指向编码表中的某个字符0或1
for (unsigned int j = 0; j < CharSetSize; j++) {
if (CharSet[j] == Read) {
pCode = HC[j + 1];
while (*pCode) {
CodeSize++;
WriteBit(&Byte, Offset, *pCode - '0');
if (Offset) {
//字节没有写满,offset-1
Offset--;
} else {
//字节写满了就写入文件,然后清空字节
Offset = 7;
fwrite(&Byte, sizeof(unsigned char), 1, fpCode);
Byte = 0;
}
pCode++;
}
Status = 0;
break;
}
}
if (Status) printf("提示:已忽略没有在字符集中出现的字符%c\n", Read);
}
//最后一个字节没有写满也要写入,没有写满的位都是0
if (Offset != 7) {
fwrite(&Byte, sizeof(unsigned char), 1, fpCode);
}
//在文件最后写入编码位数
fwrite(&CodeSize, sizeof(unsigned long long), 1, fpCode);
fclose(fpCode);
fclose(fpText);解码的操作,书上也只写了“留给读者去完成”咕咕咕,实际上过程也很简单~
- 将一个指针指向 Huffman 树的根结点。
- 读取一个个 0/1(不论是字符还是二进制位,总之读取就对了!),将指针指向结点的左/右子树。
- 指到叶子结点就输出对应的字符,然后将指针移回根结点。
其实是编码的逆过程,所以动图就不做了~想象一下倒放上面那个动图的样子就好(你连倒放动图都懒得做了嘛!( `д´ )
//读取Huffman树过程略x2
//变量定义略x2,自己判断变量类型咯~
//根据H树建立编码表
InitHuffmanCode(&HC, HT, CharSetSize);
//读取CodeFile
Index = 2 * CharSetSize - 1;
fopen_s(&fpCode, "CodeFile.bin", "rb");
fopen_s(&fpText, "TextFile.txt", "wb");
//读取编码位数
fseek(fpCode, -1L * (long)sizeof(unsigned long long), SEEK_END);
fread(&CodeSize, sizeof(unsigned long long), 1, fpCode);
fseek(fpCode, 0L, SEEK_SET);
Offset = 7;
fread(&Byte, sizeof(unsigned char), 1, fpCode); //先读取一个字节
//对CodeFile中的每个位进行读取
for (unsigned long long i = 0; i < CodeSize; i++) {
Read = ReadBit(Byte, Offset);
if (Read) {
//读到1就移向右子树
Index = HT[Index].rchild;
} else {
//读到0就移向右子树
Index = HT[Index].lchild;
}
//移到叶子结点就写入字符,同时移回根结点
if (!HT[Index].lchild && !HT[Index].rchild) {
fwrite(&CharSet[Index - 1], sizeof(char), 1, fpText);
Index = 2 * CharSetSize - 1;
}
if (Offset) {
//字节没有读完,offset-1
Offset--;
} else {
//字节读完了就读下一个字节
Offset = 7;
fread(&Byte, sizeof(unsigned char), 1, fpCode);
}
}
fclose(fpCode);
fclose(fpText);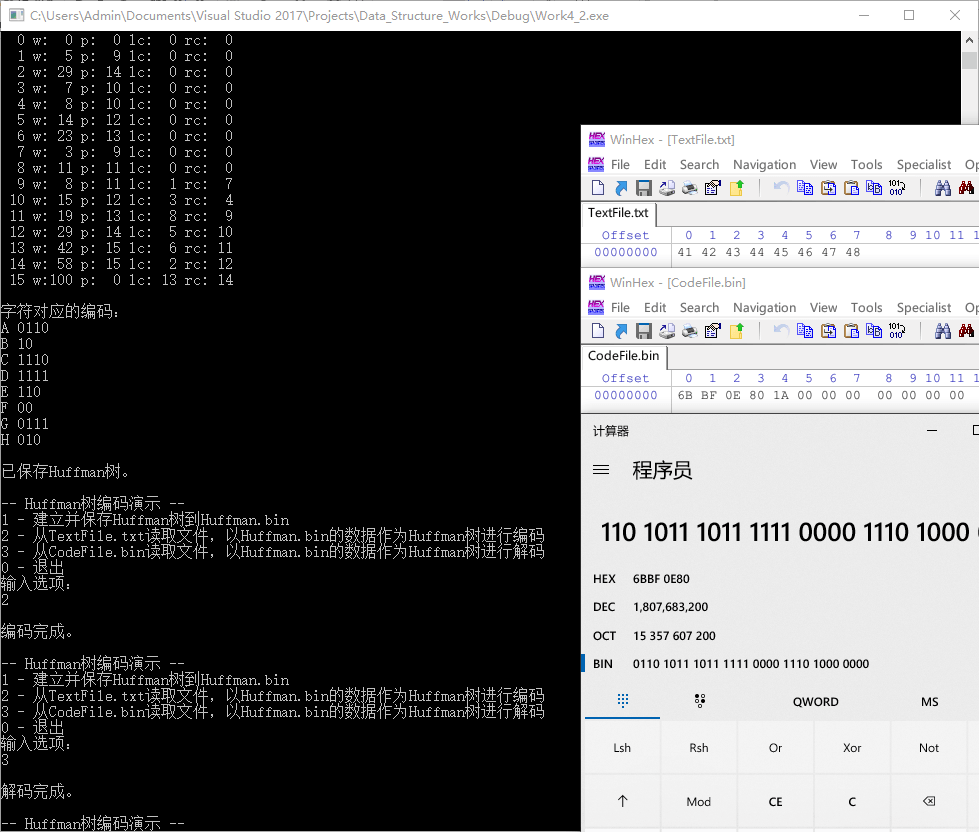
最后的效果就是上面这样。
6B BF 0E 80用二进制表示为0110 10 1110 1111 110 00 0111 010 000000,对应了ABCDEFGH的 Huffman 编码,后面的六个0是为了补全字节用的~1A用十进制表示为26,表示 Huffman 编码占用的 26 个二进制位。
完整的代码在这里了~c(ˊᗜˋ*c)
另外,这个题目只要求根据输入的一个字符集生成 Huffman 编码。不过,如果“字符集”包括了 0x00 到 0xFF 的所有字节,将“权”设为每个字节在文件中出现的次数,那不就可以用来压缩文件了吗!\(≧▽≦)/
以后有空再写这个,做出来了也会把完整的源代码丢粗来ヾ(´∀`。ヾ)
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。不允许内容农场类网站、CSDN 用户和微信公众号转载。
本文作者:✨小透明・宸✨
本文链接:https://akarin.dev/2019/04/06/huffman-tree/
