封面图：Pixiv ID: 89044985 「赤座あかりちゃん」 by たんたんめん

涉及密码学的课我没少上，而每个学期上这种课的时候都一定会把 RSA、MD5、DES、AES……这些经典算法，以及分组密码的四个经典的工作模式之类的东西轮流过一遍，顺便稍微提一下还有一类比 RSA 更好的算法叫椭圆曲线。知道这些理论后，期末考个 80 分以上基本上就不是问题了。

但是，虽然理论上的东西讲了这么多，将这些理论用到实践的机会实在是少之又少。好不容易在某课程的期末大作业里看到一个“信息的安全传输”：

用密码学手段解决文件的安全传输，有点意思。再看看后面的参考用流程图：

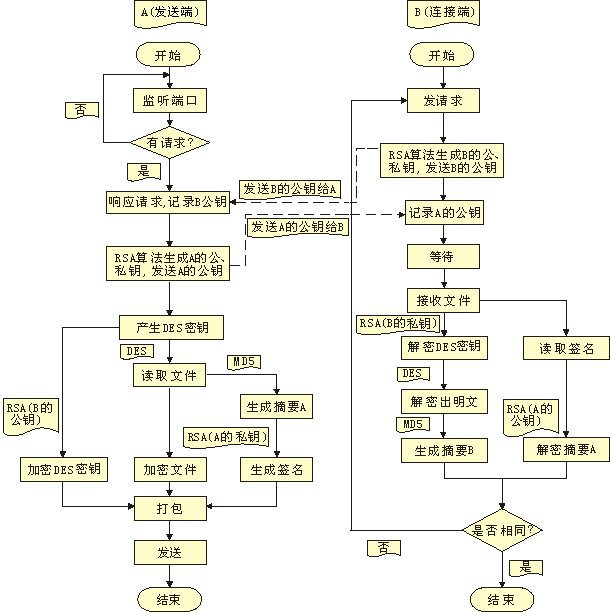
嗯……这个流程图用的都是相当经典的教科书式的操作：

• 混合加密：使用非对称密码交换会话密钥，然后在后续的数据交换中使用会话密钥和对称密码
• 密钥交换：随机生成会话密钥后，用对方的公钥加密再发过去，对方用私钥解密
• 数字签名：对数据计算 hash 后用自己的私钥签名，对方用公钥验证

如果一定要说有什么问题的话，DES 和 MD5 这两个算法已经很陈旧且不安全了，直接用 AES 和 SHA-256 之类的更现代的算法替代也不困难。但是在上面的流程中重度使用的 RSA 算法是否也可以使用更好的替代品呢？

还真的有，这就是标题里的基于 Curve25519 椭圆曲线的 X25519 密钥交换算法和 Ed25519 签名算法。

由于我姿势水平有限，所以以下的介绍可能会存在错误什么的，如果指出来的话我会修正的 (´ﾟωﾟ｀)

教科书式 RSA 的问题

众所周知，RSA 的安全性来自于“大素数分解”这一数学难题：将两个很大的素数相乘很容易，但是从相乘的积分解出这两个素数非常难，或者说在计算上是不可行的。具体的算法过程和数学证明就不再介绍，可以直接参见这里。

RSA 是非常经典的非对称密码算法，可以同时用于加密和签名，但是它最大的缺点就出在“大素数”上。如果刚刚提到的素数分解问题被解决，RSA 就没有任何安全性可言了，因此需要不断增大那两个素数的位数（一般也被叫做“密钥长度”），需要增加到什么程度呢？目前 Factordb 上已经有了 768 位的数被分解的记录，因此 1024 位也已经比较危险了，根据 NIST 的建议 2048 位的密钥可以用到 2030 年左右。

一味增加密钥长度带来的突出问题是 RSA 的执行速度被严重拖慢了，生成密钥、加密解密和签名的时间都会随着密钥长度的增加而出现指数级的延长。以生成不同长度的密钥对为例，在这里在线测试所消耗的时间如下：

• 512 位：50-100 ms
• 1024 位：500-1500 ms
• 2048 位：8000-15000 ms
• 4096 位：100000 ms 以上

生成一个安全的密钥要等十几秒，这合理吗？还好我们现在都知道应该使用混合加密了，RSA 在加密过程中只是用于一开始的密钥交换而已，而且只需要在服务端的加密系统初始化时生成一次密钥似乎就够了，慢一些也可以接受……？

遗憾的是，使用 RSA 的非对称特性进行密钥交换还存在另一个严重问题。假定有攻击者可以监听客户端和服务端双方通信的所有数据，于是他得到了公钥以及用公钥加密后的会话密钥，这些信息当然不足以让攻击者得到会话密钥从而解密后续的所有使用对称加密传输的信息。但是如果有一天服务端的私钥泄露了，攻击者就可以得到每次通信所使用的会话密钥，进而解密出所有先前监听到的通信内容。

即使不使用 RSA 而是使用另一个经典的密钥交换算法 Diffie-Hellman，只要有一方的密钥对固定不变，也会面临同样的问题。

解决办法也很简单：那就在密钥交换时让双方使用的密钥对每次都不一样好了。这样，即使某次通信时使用的私钥泄露，攻击者也只能解密这次通信的内容，而其他通信仍然是安全的。这种特性在密码学上被称为前向安全性（Perfect Forward Secrecy）（上课的时候完全没讲过这个……），顾名思义就是保护先前的通信的保密性不会受到来自未来的暴露的密钥的威胁。

Diffie-Hellman Ephemeral 就是 Diffie-Hellman 加上“每次交换时需要随机生成密钥对”这一要求后的改进算法，Ephemeral 的意思是“短暂的”。那 RSA 的密钥交换有没有对应的支持前向安全性的改进算法呢？

可以做，但是考虑上面提到的速度问题就很容易知道这样的改进对 RSA 来说并没有什么实用意义。回到上面的“文件的安全传输”流程图，你能接受每次传输文件前都要等待十几秒来生成密钥对吗？

所以和教科书里不同的是，直接使用 RSA 加密进行密钥交换实际上已经过时了。已有的 TLS 协议的密码套件中，推荐的组合里 RSA 都只是用于身份验证（也就是签名，即使私钥泄露也不影响保密性），实际的密钥交换都是通过 DHE 或椭圆曲线的 ECDHE（注意多出来的这个 E，它表示的就是 Ephemeral）完成的。

顺便一提，和教科书里所述同样不同的是，现实中使用的 RSA 加密会对数据使用 OAEP 方案进行填充。由于填充过程引入了随机数，因此用同样的密钥多次加密相同的明文的结果也是不一样的。

Curve25519 系列算法简单介绍

基于椭圆曲线的非对称密码解决了 RSA 密钥长度大，运行时间长的问题，256 位的椭圆曲线密钥可以等效于 3072 位的 RSA 密钥。目前常用的椭圆曲线密码系统是基于 NIST 系列标准的曲线（例如 P-256，又称 secp256r1 和 prime256v1）而设计的 ECDH 密钥交换算法和 ECDSA 签名算法。

虽然如此，NIST 标准曲线仍然存在一些问题。在设计密码算法时可能需要定义一些常数，这些常数应该以一种比较透明的方式选择，例如：

• MD5 算法中处理单个 512 字节输入消息分组的轮函数中用到了 64 个常数，由 floor(abs(sin(i + 1)) * (2 ** 32)) 计算得到。
• SHA1 算法的五个初始值是数字 0 到 F 在大端序下的顺序排列：0x67452301、0xEFCDAB89、0x98BADCFE、0x10325476、0xC3D2E1F0。
• ChaCha20 算法使用字符串 expand 32-byte k 的 ASCII 码填充初始的状态矩阵。

把 sin 换成 tan 之类的其他数学函数，或者修改那个字符串，对算法的安全性都不会有什么影响。常数的选择方式仅仅是为了证明在选择的过程中并没有什么特别的操作空间，无法用于预留后门之类的用途。用这类方式选择的常数被称为 Nothing-up-my-sleeve number，这个称呼来自于魔术师变魔术前张开袖子以表示自己两手空空的做法。

有些密码算法的常数选择没有遵循这一规律，从而引起了怀疑和批评，例如 NSA 设计的 DES 算法的 S 盒就没有任何的依据（后来才有研究发现实际上是为了抵御差分密码分析），另一个更严重的例子是 NIST 推荐的伪随机数生成器 Dual_EC_DRBG 也使用了没有选择依据的常数，被斯诺登曝光出存在 NSA 设计的后门。在这些先例下，当 NIST 标准曲线的系数也出现了来历不明的一系列常数时，它的安全性也就值得怀疑了。

另一个问题是，ECDSA 签名算法中使用了随机数，这使得使用相同的密钥多次对相同的明文签名的结果也会不一样：

$private = openssl_pkey_new([
    'private_key_type' => OPENSSL_KEYTYPE_EC,
    'curve_name' => 'prime256v1',
]);
$public = openssl_pkey_get_details($private)['key'];
$message = 'test';

for ($i = 0; $i < 3; $i++) {
    openssl_sign($message, $sign, $private, OPENSSL_ALGO_SHA256);
    var_dump(bin2hex($sign), openssl_verify($message, $sign, $public, OPENSSL_ALGO_SHA256));
}

// string(144) "3046022100a6fc5cda8b435e777a4a7342e4777930184816af02579c08f7d633f208571951022100ddd6c9647a5a9f2905c355ce9cd11e4b26d6b4e08afd6d853270b5c3958d5447"
// int(1)
// string(140) "304402207e25def883eb91e663aa8f09de1f373bf673cb8f989ed2459591e4e716200f5e02206118a1e1efe17fca6632fff3fbb1b605e162bc57023cb99b9bdfe12b19ac95b6"
// int(1)
// string(142) "3045022100d2effb78a5375dc1f1c1603121c312d7b56987bcd5f19a92d37ecc49438f4fad02207cf83ea53494f4a1cc77c04ba945c4c593cc306b9b68e4e63eb9fd4ebd9ee0e8"
// int(1)

如果签名时使用的随机数发生器存在缺陷，在两次签名中输出了相同的随机数，就存在使用签名恢复出私钥的可能（参见这篇文章的介绍及它的译文）。

由密码学家 Daniel J. Bernstein 在 2006 年独立设计的基于 Curve25519 曲线的 X25519 密钥交换算法 和 Ed25519 签名算法正好避开了以上的 NIST 标准曲线存在的问题，安全性同样等效于 3072 位 RSA，还有以下的优点：

• 速度快，当然椭圆曲线密码都能做到这个。
• 数据量小，公钥和私钥仅 32 字节，签名仅 64 字节，椭圆曲线密码也应该能做到这个。
• 算法的设计和参数选择是明确的，作者自己撰写了相关论文作为依据。
• 在算法中回避了分支操作，可以防止时序攻击（Timing Attack）。
• 任何一个 32 字节的随机值都可以作为私钥，不需要另外选取或验证。
• Ed25519 是确定性签名算法，不使用随机数，对于相同的私钥和明文可以得到相同的签名。

Curve25519 系列算法在 2006 年提出，但直到“棱镜门”曝光出 NIST 标准算法可能存在后门之后才开始流行起来。目前 OpenSSH 就已经支持生成 Ed25519 密钥并用于公钥登录：

ssh-keygen -t ed25519

2018 年推出的最新的 TLS 1.3 标准支持使用 X25519 和使用 NIST 标准曲线的 ECDHE 进行密钥交换（顺便把 RSA 密钥交换砍掉了），但是据我观察，浏览器似乎都首选使用 X25519。另外 Ed25519 也是 TLS 1.3 支持的签名算法之一。

在 libsodium 中使用 Curve25519 系列算法，以 PHP 的 Sodium 扩展为例

Daniel J. Bernstein 给出了 X25519 和 Ed25519 的 C 语言实现，不过他还将这两个算法和 ChaCha20Poly1305、AES-256-GCM、HMAC-SHA-256 等比较现代的密码算法放在一起，做了个名为 Networking and Cryptography library 的开源加密库，简称 NaCl，读作 Salt。密码学中有“盐”的概念，食盐的主要成分也是 NaCl，我有点怀疑这个名字是为了玩梗而强行凑出来的……

NaCl 已经停止更新了，有人在 NaCl 的基础上开了名为 libsodium 的分支继续改进，这个分支的名字大概也是为了照应 NaCl 而取的……总之需要在代码里使用 X25519 和 Ed25519 的话，可以使用 libsodium 以及各种编程语言对它的 binding。

libsodium 的设计尽可能地隐藏了加密算法的实现细节，从它的函数名就可以看出来。例如包含了 X25519 密钥交换和 ChaCha20Poly1305 认证加密的相关函数统一称为 crypto_box_*，使用 BLAKE2b 进行 hash 的相关函数统一称为 crypto_generichash_*，都不涉及到具体的算法名称。

这里我还是选择 PHP 作为使用例。从 PHP 7.2 开始 Sodium 扩展已经随 PHP 本体一起附带了，在系统里安装了 libsodium 的条件下即可使用。如果是使用 C 语言编写的原版或其它 binding 的话，用到的函数名称应该是差不多的。

X25519 的使用

从私钥生成公钥需要用到 sodium_crypto_scalarmult_base，使用自己的私钥和对方的公钥进行密钥交换需要用到 sodium_crypto_scalarmult。前面提过 Curve25519 系列算法可以使用任意的 32 字节作为私钥，所以可以从密码学安全的伪随机数生成器（CSPRNG）自行生成私钥。我这里作为演示就直接使用了 X25519 的标准测试向量：

// 实际使用时必须随机生成私钥：
// $private = random_bytes(32);
$privateA = hex2bin('77076d0a7318a57d3c16c17251b26645df4c2f87ebc0992ab177fba51db92c2a');
$privateB = hex2bin('5dab087e624a8a4b79e17f8b83800ee66f3bb1292618b6fd1c2f8b27ff88e0eb');
$publicA = sodium_crypto_scalarmult_base($privateA);
$publicB = sodium_crypto_scalarmult_base($privateB);
$sharedA = sodium_crypto_scalarmult($privateA, $publicB);
$sharedB = sodium_crypto_scalarmult($privateB, $publicA);
assert($sharedA === $sharedB);
var_dump(bin2hex($sharedA));

// string(64) "4a5d9d5ba4ce2de1728e3bf480350f25e07e21c947d19e3376f09b3c1e161742"

也可以使用 sodium_crypto_box_keypair 直接生成密钥对，得到一个 64 字节的字符串，前半和后半分别是私钥和公钥，可以用 substr 或 sodium_crypto_box_secretkey 和 sodium_crypto_box_publickey 提取。

虽然前面提过可以使用任意 32 字节作为私钥，实际使用时还会进行 clamp 处理。将整个 32 字节当成是小端序表示的 256 位整数，clamp 等效于将这个数的最低三位设成 000（强制设为 8 的倍数）以及将最高两位设成 01：

k[0]  &= 248; // 0b11111000;
k[31] &= 127; // 0b01111111;
k[31] |=  64; // 0b01000000;

这两个操作分别是为了避免小子群攻击和保证算法在常数时间内完成以避免时序攻击（稍微详细一些的解释在这里）。不过实际使用的时候各种实现会自动进行 clamp，因此不需要手动操作：

// 把$privateA[31]从0x2A 0b00101010改成0xAA 0b10101010（最高两位设成10）
$privateA = hex2bin('77076d0a7318a57d3c16c17251b26645df4c2f87ebc0992ab177fba51db92caa');
// 把$privateB[0]从0x5D 0b01011101改成0x5F 0b01011111（最低两位设成111）
$privateB = hex2bin('5fab087e624a8a4b79e17f8b83800ee66f3bb1292618b6fd1c2f8b27ff88e0eb');
$publicA = sodium_crypto_scalarmult_base($privateA);
$publicB = sodium_crypto_scalarmult_base($privateB);
$sharedA = sodium_crypto_scalarmult($privateA, $publicB);
$sharedB = sodium_crypto_scalarmult($privateB, $publicA);
assert($sharedA === $sharedB);
var_dump(bin2hex($sharedA));

// string(64) "4a5d9d5ba4ce2de1728e3bf480350f25e07e21c947d19e3376f09b3c1e161742"
// 密钥交换结果没有变化

X25519 输出了 32 字节的共享密钥，但是 libsodium 不建议将这 32 字节直接作为密钥使用，推荐的做法是将它与双方的公钥一起进行 hash 处理。根据考证，TLS 中也有类似的做法：密钥交换得到的共享密钥被称为 Pre Master Secret，同样需要与双方的公钥 Client/Server Random 一起输入密钥派生函数（TLS 1.2 及以前为 PRF，TLS 1.3 改为 HKDF），得到最终使用的会话密钥 Master Secret。

至于为什么还要进行一次密钥派生，根据 Stack Overflow 上的两个回答（这个和这个），主要是出于以下的理由：

• 可以将密钥交换和生成会话密钥的过程各自独立出来。
• 使通信双方都能对会话密钥的生成过程产生影响。
• 不同密钥交换算法产生的共享密钥长度可能不一样，也不一定和会话密钥固定要求的长度相同。
• 某些密钥交换算法产生的共享密钥存在随机分布不均的情况。

对于最后一点，实际上 X25519 输出的共享密钥也存在这个问题。如果注意一下共享密钥中各位出现 0 或 1 的次数，就会发现密钥的最后一个字节的最高位固定为 0，其他位出现 0 和 1 的次数则基本相同：

$bits = [
    [0, 0], [0, 0], [0, 0], [0, 0],
    [0, 0], [0, 0], [0, 0], [0, 0],
];
for ($i = 0; $i < 1024; $i++) {
    $privateA = random_bytes(32);
    $privateB = random_bytes(32);
    $publicA = sodium_crypto_scalarmult_base($privateA);
    $publicB = sodium_crypto_scalarmult_base($privateB);
    $sharedA = sodium_crypto_scalarmult($privateA, $publicB);
    $sharedB = sodium_crypto_scalarmult($privateB, $publicA);
    assert($sharedA === $sharedB);

    $byte = ord($sharedA[31]);
    for ($j = 0; $j < 8; $j++) {
        $bits[$j][(int)(bool)($byte & (1 << $j))]++;
    }
}
var_dump($bits);

// array(8) {
//   [0] => array(2) { [0] => int(493) [1] => int(531) }
//   [1] => array(2) { [0] => int(527) [1] => int(497) }
//   [2] => array(2) { [0] => int(496) [1] => int(528) }
//   [3] => array(2) { [0] => int(547) [1] => int(477) }
//   [4] => array(2) { [0] => int(520) [1] => int(504) }
//   [5] => array(2) { [0] => int(531) [1] => int(493) }
//   [6] => array(2) { [0] => int(498) [1] => int(526) }
//   [7] => array(2) { [0] => int(1024) [1] => int(0) }
// }

因此进行密钥派生是有必要的。

Ed25519 的使用

Ed25519 签名的相关函数统一称为 sodium_crypto_sign_*，主要用到以下函数：

• 直接生成密钥对：sodium_crypto_sign_keypair
• 从私钥生成密钥对：sodium_crypto_sign_seed_keypair
• 从密钥对中提取私钥和公钥：sodium_crypto_sign_secretkey、sodium_crypto_sign_publickey
• 签名：sodium_crypto_sign_detached
• 验证：sodium_crypto_sign_verify_detached

同样使用 Ed25519 的标准测试向量作为演示：

$private = sodium_crypto_sign_seed_keypair(
    hex2bin('833fe62409237b9d62ec77587520911e9a759cec1d19755b7da901b96dca3d42')
);
$message = hex2bin(''
    . 'ddaf35a193617abacc417349ae204131'
    . '12e6fa4e89a97ea20a9eeee64b55d39a'
    . '2192992a274fc1a836ba3c23a3feebbd'
    . '454d4423643ce80e2a9ac94fa54ca49f'
);
$sign = sodium_crypto_sign_detached($message, sodium_crypto_sign_secretkey($private));
$public = sodium_crypto_sign_publickey($private);
assert(sodium_crypto_sign_verify_detached($sign, $message, $public));
var_dump(bin2hex($public), bin2hex($sign));

// string(64) "ec172b93ad5e563bf4932c70e1245034c35467ef2efd4d64ebf819683467e2bf"
// string(128) "dc2a4459e7369633a52b1bf277839a00201009a3efbf3ecb69bea2186c26b58909351fc9ac90b3ecfdfbc7c66431e0303dca179c138ac17ad9bef1177331a704"

这里的密钥对长度为 96 字节，前 64 字节为私钥，后 32 字节为公钥，但是私钥的后 32 字节和公钥是一模一样的……

Ed25519 的算法中也存在 clamp 处理，但是处理的对象是算法内部对私钥计算 SHA-512 后的值，因此也不需要手动操作，改变私钥的话签名结果一定会改变。

顺便一提，签名是为了保证消息的完整性。教科书里提到签名的做法一般都是对明文/密文计算 hash 然后对 hash 签名，或者是对明文计算 hash 然后将 hash 和明文一起加密，方法很多，但是自己和加密算法组合的话容易出错。作为改进，后来出现了一类称为“认证加密”（Authenticated Encryption with Associated Data）的算法，可以在不另外使用签名的情况下同样保证完整性。认证加密与一般的加密的区别在于：

• 加密时，除明文和密钥外，还需要输入“附加的认证信息”（Associated Authenticated Data）。
• 加密后，除了密文还会得到一定长度的消息认证码 MAC，需要随密文一起发送出去。
• 解密时，需要输入相同的认证信息和加密得到的 MAC 进行验证，如果密文被篡改则会导致验证失败。

常见的认证加密算法包括 AES-GCM 和 ChaCha20Poly1305 等，如果使用了认证加密算法就不需要另外进行签名了。

在 OpenSSL 中使用 Curve25519 算法

作为加密库，libsodium 比较小众，相比之下还是 OpenSSL 有更广泛的使用。除了在各大 Linux 发行版里已有预装，大多数编程语言也内置了相应的 binding，比如 PHP 中同样是随本体一起附带的同名扩展，Node.js 自带的 crypto 模块就是对 OpenSSL 的封装。

OpenSSL 从 1.1.0 和 1.1.1 开始分别加入了对 X25519 和 Ed25519 的支持，不过 binding 不一定都能跟进，PHP 的 OpenSSL 扩展就仍然没有提供相关的功能（再吐槽一下，它虽然支持 ChaCha20Poly1305 的加密解密，但是并没有被当成一种认证加密算法来使用，也就无法获取和验证 MAC，这个问题从 PHP 7.2 开始提出三年了都还没有解决），Node.js 的 crypto 倒是已经支持了，至于其他语言的 binding 我反而没用过，在另一个常用的语言 Python 那边我用得最多的加密库不是 pyOpenSSL 而是 PyCryptodome，后者和 OpenSSL 毫无关系而且也只支持 NIST 标准曲线而不支持 Curve25519……

总之下面先用 OpenSSL 的 CLI 作为 X25519 的使用例好了。

对于 X25519 密钥交换，参考 Stack Overflow 上的这个回答，稍微改一改使用的算法就可以了。首先是生成私钥：

openssl genpkey -algorithm x25519 -out alice.der -outform der
openssl genpkey -algorithm x25519 -out bob.der -outform der
cat alice.der | od -t x1
cat bob.der | od -t x1
# 0000000 30 2e 02 01 00 30 05 06 03 2b 65 6e 04 22 04 20
# 0000020 f8 fe 42 87 cc 79 8a 8b b9 1b fc 71 16 fc 75 32
# 0000040 e3 4f 63 06 07 e4 fc 46 75 1d 1e d8 63 96 7e 48
# 0000060
# 0000000 30 2e 02 01 00 30 05 06 03 2b 65 6e 04 22 04 20
# 0000020 00 f9 28 97 40 10 c9 9d c0 56 76 b9 bf ae a3 a2
# 0000040 3c 67 8d 8e 13 10 15 5e 36 c4 ba ed 28 16 83 58
# 0000060

嗯？X25519 的公私钥都是 32 字节的，怎么这里输出了 48 字节的东西？

因为那 32 字节是原始的密钥，而 OpenSSL 使用的是实际应用中封装了包括但不限于算法名称、数学参数、版本号、序列号、有效期等等信息的 X.509 或 PKCS 标准的证书格式，这些内容在证书里又按照 ASN.1 标准被序列化。直接保存序列化后得到的二进制数据的证书格式叫做 DER，考虑到使用二进制数据时可能存在不便，因此还有另一种等效的 PEM 格式，这种格式以字符串 -----BEGIN/END ...----- 开头/结尾，将二进制数据通过 Base64 编码后存在中间。上面输出的就是 DER 格式的私钥。平时使用 https 上网时，浏览器收到的服务端的证书就是这类格式的。

那这 48 字节包括了什么信息呢？找个在线的 ASN.1 解析器查看一下：

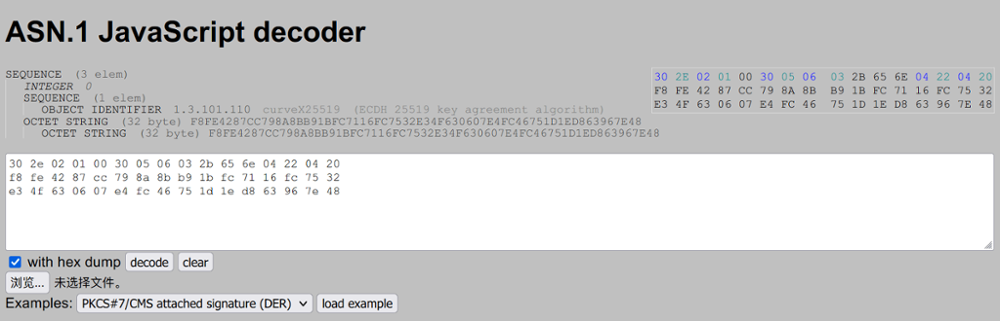
这些数据使用的是 PKCS#8 格式，添加了 X25519 的算法标识和一些结构信息，不难注意到前 16 字节是固定的，后 32 字节就是私钥本身，因此其实也可以把固定的前 16 字节 30 2e 02 01 00 30 05 06 03 2b 65 6e 04 22 04 20 抽出来，然后自己从 CSPRNG 里取出 32 字节拼接到一起：

# openssl genpkey -algorithm x25519 -out alice.der -outform der
# openssl genpkey -algorithm x25519 -out bob.der -outform der

# 30 2e 02 01 00 30 05 06 03 2b 65 6e 04 22 04 20
echo -n "MC4CAQAwBQYDK2VuBCIEIA==" | base64 -d > alice.der
echo -n "MC4CAQAwBQYDK2VuBCIEIA==" | base64 -d > bob.der
dd if=/dev/urandom bs=32 count=1 >> alice.der
dd if=/dev/urandom bs=32 count=1 >> bob.der

然后是从私钥生成公钥：

openssl pkey -pubout -in alice.der -out alice.pub -inform der -outform der
openssl pkey -pubout -in bob.der -out bob.pub -inform der -outform der
cat alice.pub | od -t x1
cat bob.pub | od -t x1
# 0000000 30 2a 30 05 06 03 2b 65 6e 03 21 00 23 1b c3 9e
# 0000020 38 65 a8 e4 b9 1c e9 de 37 7f a2 8b 9f 06 ad 64
# 0000040 83 79 24 86 d3 ca 41 08 26 67 6c 38
# 0000054
# 0000000 30 2a 30 05 06 03 2b 65 6e 03 21 00 1b 39 77 8a
# 0000020 f5 cd 2d 61 2f 49 4d 91 94 6c ce ee b1 e5 bc e9
# 0000040 6f 65 03 02 c1 21 c5 76 4f 2c 99 0b
# 0000054

同理，这里的二进制数据使用的是 SPKI 格式，固定的前 12 字节 30 2a 30 05 06 03 2b 65 6e 03 21 00 可以抽出来，和从 libsodium 或是别的方式收到的 32 字节公钥拼起来。

最后是密钥交换，这次得到的就直接是 32 字节的共享密钥了：

openssl pkeyutl -derive -out alicebob.key -inkey alice.der -peerkey bob.pub -keyform der -peerform der
openssl pkeyutl -derive -out bobalice.key -inkey bob.der -peerkey alice.pub -keyform der -peerform der
cmp alicebob.key bobalice.key
cat alicebob.key | od -t x1
cat bobalice.key | od -t x1
# 0000000 01 e0 1d 2b 07 d7 c0 1d e9 28 ef c2 ea b7 f6 a0
# 0000020 6b 27 ab fa dc 73 52 f7 58 92 de 2b cd d0 cd 44
# 0000040
# 0000000 01 e0 1d 2b 07 d7 c0 1d e9 28 ef c2 ea b7 f6 a0
# 0000020 6b 27 ab fa dc 73 52 f7 58 92 de 2b cd d0 cd 44
# 0000040

至于在 CLI 中使用 Ed25519 签名……签名和验证的功能并没有加入 CLI，原因是 RSA 和 ECDSA 签名都是先要另外选择一种算法对消息计算 hash 后再使用算法对 hash 签名，但是 Ed25519 不需要这么做，而是直接将消息输入签名算法，在算法内部钦定了使用 SHA-512 计算 hash 然后进行后续操作。由于“输入算法的是消息的 hash 还是本体”这一过程存在不同，因此 OpenSSL 一开始没有将 Ed25519 签名和验证加入 CLI（在 3.0.0 中加入了，不过这个版本刚发布没多久而且可能存在不兼容的变更，因此我没有自己使用这个版本进行测试），但是源代码还是支持的。

openssl/doc/man1/pkeyutl.pod

The Ed25519 and Ed448 signature algorithms are not supported by this utility. They accept non-hashed input, but this utility can only be used to sign hashed input.

当然生成密钥对还是支持的：

openssl genpkey -algorithm ed25519 -out private.der -outform der
cat private.der | od -t x1
# 0000000 30 2e 02 01 00 30 05 06 03 2b 65 70 04 22 04 20
# 0000020 8a da 59 23 d4 7d a0 ed 36 c8 a6 6e 26 26 3a 75
# 0000040 b4 a4 f7 48 91 5a 8e c3 7f 45 71 8b 38 f1 da 8b
# 0000060

openssl pkey -pubout -in private.der -out public.pub -inform der -outform der
cat public.pub | od -t x1
# 0000000 30 2a 30 05 06 03 2b 65 70 03 21 00 e1 42 2a ee
# 0000020 ec 89 33 41 96 74 fd 6d ec d6 a7 69 94 2b 58 1d
# 0000040 5e 37 e4 d2 e8 f8 d6 41 79 3d 97 a4
# 0000054

仍然可以提取出私钥和公钥的前几个字节和原始的密钥拼接，私钥的前 16 个字节是 30 2e 02 01 00 30 05 06 03 2b 65 70 04 22 04 20，公钥的前 12 个字节是 30 2a 30 05 06 03 2b 65 70 03 21 00，其实只是算法标识不同而已。

再附加一个在 Node.js 中通过 crypto 模块使用 X25519 和 Ed25519 的例子，使用的还是前面的标准测试向量，因为太长所以这里就折叠了：

const crypto = require('crypto');

const x25519PrivateKeyPkcs8Header = Buffer.from('302e020100300506032b656e04220420', 'hex');
const x25519PublicKeySpkiHeader = Buffer.from('302a300506032b656e032100', 'hex');

// const {
//     privateKey: privateKeyA,
//     publicKey: publicKeyA,
// } = crypto.generateKeyPairSync('x25519');
// const {
//     privateKey: privateKeyB,
//     publicKey: publicKeyB,
// } = crypto.generateKeyPairSync('x25519');

const privateKeyA = crypto.createPrivateKey({
    key: Buffer.concat([
        x25519PrivateKeyPkcs8Header,
        Buffer.from(
            '77076d0a7318a57d3c16c17251b26645df4c2f87ebc0992ab177fba51db92c2a',
            'hex'
        ),
    ]),
    format: 'der',
    type: 'pkcs8',
});
const privateKeyB = crypto.createPrivateKey({
    key: Buffer.concat([
        x25519PrivateKeyPkcs8Header,
        Buffer.from(
            '5dab087e624a8a4b79e17f8b83800ee66f3bb1292618b6fd1c2f8b27ff88e0eb',
            'hex'
        ),
    ]),
    format: 'der',
    type: 'pkcs8',
});
// const publicKeyA = crypto.createPublicKey({ key: privateKeyA });
// const publicKeyB = crypto.createPublicKey({ key: privateKeyB });
const publicKeyA = crypto.createPublicKey({
    key: Buffer.concat([
        x25519PublicKeySpkiHeader,
        Buffer.from(
            '8520f0098930a754748b7ddcb43ef75a0dbf3a0d26381af4eba4a98eaa9b4e6a',
            'hex'
        )
    ]),
    format: 'der',
    type: 'spki',
});
const publicKeyB = crypto.createPublicKey({
    key: Buffer.concat([
        x25519PublicKeySpkiHeader,
        Buffer.from(
            'de9edb7d7b7dc1b4d35b61c2ece435373f8343c85b78674dadfc7e146f882b4f',
            'hex'
        )
    ]),
    format: 'der',
    type: 'spki',
});

const sharedA = crypto.diffieHellman({
    privateKey: privateKeyA,
    publicKey: publicKeyB,
});
const sharedB = crypto.diffieHellman({
    privateKey: privateKeyB,
    publicKey: publicKeyA,
});
console.log(sharedA.equals(sharedB));
console.log(sharedA);
// true
// 4a5d9d5ba4ce2de1728e3bf480350f25e07e21c947d19e3376f09b3c1e161742

const crypto = require('crypto');

const ed25519PrivateKeyPkcs8Header = Buffer.from('302e020100300506032b657004220420', 'hex');
const ed25519PublicKeySpkiHeader = Buffer.from('302a300506032b6570032100', 'hex');

// const { privateKey, publicKey } = crypto.generateKeyPairSync('ed25519');

const privateKey = crypto.createPrivateKey({
    key: Buffer.concat([
        ed25519PrivateKeyPkcs8Header,
        Buffer.from(
            '833fe62409237b9d62ec77587520911e9a759cec1d19755b7da901b96dca3d42',
            'hex'
        ),
    ]),
    format: 'der',
    type: 'pkcs8',
});
// const publicKey = crypto.createPublicKey({ key: privateKey });
const publicKey = crypto.createPublicKey({
    key: Buffer.concat([
        ed25519PublicKeySpkiHeader,
        Buffer.from(
            'ec172b93ad5e563bf4932c70e1245034c35467ef2efd4d64ebf819683467e2bf',
            'hex'
        )
    ]),
    format: 'der',
    type: 'spki',
});
const message = Buffer.from(
    'ddaf35a193617abacc417349ae20413112e6fa4e89a97ea20a9eeee64b55d39a' +
    '2192992a274fc1a836ba3c23a3feebbd454d4423643ce80e2a9ac94fa54ca49f',
    'hex'
);
const sign = crypto.sign(null, message, privateKey)
console.log(sign.toString('hex'));
console.log(crypto.verify(null, message, publicKey, sign));
// dc2a4459e7369633a52b1bf277839a00201009a3efbf3ecb69bea2186c26b58909351fc9ac90b3ecfdfbc7c66431e0303dca179c138ac17ad9bef1177331a704
// true

最后再记录一下我把“信息的安全传输”这个大作业的流程修改成了什么样子，首先是密钥交换阶段：

1. 客户端和服务端预先生成 Ed25519 密钥对。
2. 客户端和服务端建立连接，服务端发送自己的 Ed25519 公钥，客户端可以选择是否信任。
   • 由于没有 CA，所以客户端只能自己确认收到的服务端公钥是否正确了。
   • 这个参考的是 SSH 登录的流程，第一次登录时也会显示出服务端的公钥，如果客户端不信任或是收到的公钥和之前信任的不同则会终止连接。
3. 客户端发送自己的 Ed25519 公钥，服务端可以无条件信任或根据一个白名单决定是否信任。
4. 双方各自生成 X25519 密钥对，然后互相交换公钥和时间戳以及对这两项的组合生成的签名。
   • 添加时间戳是为了防止重放攻击，其实还应该再加一个 nonce。
5. 确认签名无误后，双方使用密钥派生算法产生会话密钥和认证加密的认证信息，创建 ChaCha20Poly1305 加密/解密上下文。

然后是传输文件阶段：

1. 客户端发送文件名、文件大小等元数据，服务端进行检验并创建文件。
2. 客户端分块读取文件，加密后发送，服务端解密并写入文件。
3. 客户端发送完文件后发送 MAC，服务端验证。如果验证失败则删除文件并提示。

流程图是当时写实验报告时做的 ε-(•́ω•̀๑)

其实如果都是在桌面端使用的话应该使用 AES-GCM 的……因为桌面端都有 AES 指令集。比较加密速度的话，同样是 256 位密钥的对称加密，使用指令集的 AES 最快，其次是 ChaCha20Poly1305，不使用指令集的 AES 最慢。

本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。不允许内容农场类网站、CSDN 用户和微信公众号转载。
本文作者：✨小透明・宸✨
本文链接：https://akarin.dev/2021/09/16/a-taste-of-curve25519/